이번 장에서는 과대적합을 판단하기 위하여 검증 세트의 손실 함수 값을 함께 표시해보고, 과대적합의 해결 방법으로 드롭아웃을 배웠습니다. 또한, 이미 훈련한 모델을 저장해서 불러오는 방법과 모델의 가장 좋은 결과를 저장하고 모델을 조기종료하는 콜백도 배웠습니다.
1. 검증 세트의 손실 곡선 그리기
epoch가 늘어날수록 훈련 세트의 손실 함수 값은 낮아지게 되는데, 이것만으로는 모델 성능의 지표가 될 수 없습니다. 따라서 검증 세트의 손실 함수 값도 함께 확인하여 모델의 성능이 어떠한지 알아봅시다.
1
2
3
4
5
model = model_fn()
model.compile(loss='sparse_categorical_crossentropy', metrics='accuracy')
history = model.fit(train_scaled, train_target, epochs=20, verbose=0,
validation_data=(val_scaled, val_target))
모델을 훈련할 때 validation_data에 검증 세트의 데이터와 타깃을 튜플 형식으로 넣어주면 history.history에 val_loss와 val_accuracy도 함께 기록됩니다.
1
2
3
4
5
6
plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
plt.xlabel('epoch')
plt.ylabel('loss')
plt.legend(['train', 'val'])
plt.show()
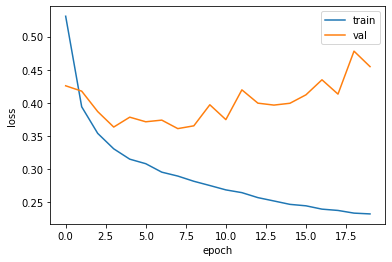
곡선을 그려 보면 epoch가 늘어날수록 오히려 검증 세트의 손실 곡선은 상승하는 과대적합된 모습을 보이고 있습니다. 옵티마이저를 adam으로 바꾸어주면 일반적으로 더 나은 결과를 얻을 수 있기 때문에 옵티마이저를 바꾼 후 다시 훈련한 후 곡선을 그려 봅시다.
1
2
3
4
5
6
7
8
9
10
11
12
13
model = model_fn()
model.compile(optimizer='adam', loss='sparse_categorical_crossentropy',
metrics='accuracy')
history = model.fit(train_scaled, train_target, epochs=20, verbose=0,
validation_data=(val_scaled, val_target))
plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
plt.xlabel('epoch')
plt.ylabel('loss')
plt.legend(['train', 'val'])
plt.show()
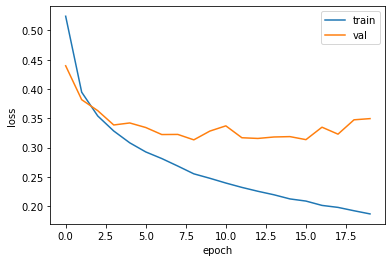
여전히 곡선은 epoch 20 이후로 약간의 상승세가 보이지만 그래도 이전보다는 낫다는 것을 눈으로 잘 확인할 수 있습니다.
2. 드롭아웃
책에서는 모델의 과대적합을 방지하는 방법으로 드롭아웃을 제시하였습니다. 드롭아웃을 적용하는 방법은 모델에 다음과 같은 드롭아웃 층을 추가하는 것입니다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
model = model_fn(keras.layers.Dropout(0.3))
model.summary()
=>Model: "sequential_4"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
flatten_4 (Flatten) (None, 784) 0
dense_8 (Dense) (None, 100) 78500
dropout (Dropout) (None, 100) 0
dense_9 (Dense) (None, 10) 1010
=================================================================
Total params: 79,510
Trainable params: 79,510
Non-trainable params: 0
_________________________________________________________________
다만, flatten 층과 같이 파라미터 수는 0인 층으로, 모델의 전체 층을 말할 때에 포함되지는 않습니다.
드롭아웃은 은닉층의 임의의 출력값들의 출력을 0으로 만들어 주는 것으로, 임의로 모델의 출력이 없어지므로 한 특성에 의지하지 않고 조금 더 일반성이 높은 모델을 만들 것이라고 기대해볼 수 있습니다. 드롭아웃을 적용한다고 해서 출력이 사라지는 것은 아니고, 값만 0이 됩니다.
드롭아웃을 적용하였을 때의 손실 곡선은 다음과 같이 그려집니다.
1
2
3
4
5
6
7
8
9
10
11
12
model.compile(optimizer='adam', loss='sparse_categorical_crossentropy',
metrics='accuracy')
history = model.fit(train_scaled, train_target, epochs=20, verbose=0,
validation_data=(val_scaled, val_target))
plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
plt.xlabel('epoch')
plt.ylabel('loss')
plt.legend(['train', 'val'])
plt.show()
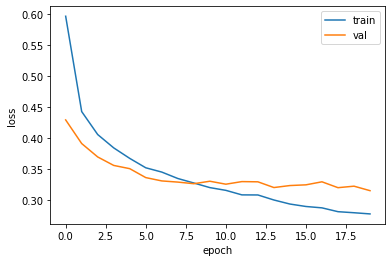
드롭아웃을 적용하지 않은 모델과 비교했을 때 상당 부분 과대적합이 해결된 모습입니다.
3. 모델 저장과 복원
1
2
3
4
5
6
model = model_fn(keras.layers.Dropout(0.3))
model.compile(optimizer='adam', loss='sparse_categorical_crossentropy',
metrics='accuracy')
history = model.fit(train_scaled, train_target, epochs=10, verbose=0,
validation_data=(val_scaled, val_target))
이제 훈련된 모델을 저장해 봅시다.
모델을 저장하는 방법에는 두 가지가 있는데, 모델의 파라미터만 저장하는 save_weights와 구조까지 전부 저장하는 save입니다.
(1) save_weights
1
model.save_weights('model-weights.h5')
이렇게 모델을 저장하면 짝이 되는 load_weights로 불러왔을 때 모델의 파라미터들만 불러오게 됩니다.
1
2
3
model = model_fn(keras.layers.Dropout(0.3))
model.load_weights('model-weights.h5')
이때 주의할 점은 이 방식으로 파마리터를 불러오려면 원래 모델과 모델의 구조가 같아야 한다는 것입니다.
또한, 모델을 훈련하기 위해서는 다시 compile부터 해야 하는데, 만약 평가만 하고자 한다면 evaluate 명령어를 쓸 수가 없습니다.
1
2
3
4
5
import numpy as np
val_labels = np.argmax(model.predict(val_scaled), axis=-1)
print(np.mean(val_labels == val_target))
=>0.8825
따라서, 수동으로 코드를 작성해 평가하였습니다.
(2) save
1
model.save('model-whole.h5')
이와 같이 모델을 저장하면 짝을 이루는 load_model로 모델을 불러올 수 있습니다.
1
2
3
4
5
model = keras.models.load_model('model-whole.h5')
model.evaluate(val_scaled, val_target)
=>375/375 [==============================] - 1s 2ms/step - loss: 0.3327 - accuracy: 0.8825
[0.33268266916275024, 0.8824999928474426]
이 경우에는 evaluate 명령어를 사용할 수 있습니다.
4. 콜백
(1) checkpoint_cb
1
2
3
4
5
6
7
8
9
10
model = model_fn(keras.layers.Dropout(0.3))
model.compile(optimizer='adam', loss='sparse_categorical_crossentropy',
metrics='accuracy')
checkpoint_cb = keras.callbacks.ModelCheckpoint('best-model.h5',
save_best_only=True)
model.fit(train_scaled, train_target, epochs=20, verbose=0,
validation_data=(val_scaled, val_target),
callbacks=[checkpoint_cb])
checkpoint_cb는 epoch 단위로 모델을 저장합니다. 그중에서도 save_best_only를 True로 하면 가장 최적의 모델만을 저장합니다.
1
2
3
4
5
model = keras.models.load_model('best-model.h5')
model.evaluate(val_scaled, val_target)
=>375/375 [==============================] - 1s 2ms/step - loss: 0.3148 - accuracy: 0.8902
[0.31479981541633606, 0.8901666402816772]
이처럼 저장된 모델을 불러와서 사용하면 다시 훈련하지 않고도 최적의 모델을 사용할 수 있게 됩니다.
(2) early_stopping_cb
early_stopping_cb는 조기종료를 시켜주는 콜백입니다. patience에 자연수를 지정해 주면 해당 횟수만큼 연속해서 손실함수 값이 개선되지 않으면 훈련을 종료합니다. 그리고 restore_best_weights를 True로 지정하면 훈련이 종료된 후 모델의 파라미터를 최적의 모델일 때의 파라미터로 돌려 줍니다.
1
2
3
4
5
6
7
8
9
10
11
12
model = model_fn(keras.layers.Dropout(0.3))
model.compile(optimizer='adam', loss='sparse_categorical_crossentropy',
metrics='accuracy')
checkpoint_cb = keras.callbacks.ModelCheckpoint('best-model.h5',
save_best_only=True)
early_stopping_cb = keras.callbacks.EarlyStopping(patience=2,
restore_best_weights=True)
history = model.fit(train_scaled, train_target, epochs=20, verbose=0,
validation_data=(val_scaled, val_target),
callbacks=[checkpoint_cb, early_stopping_cb])
책에서는 이 콜백을 checkpoint_cb와 같이 활용하였습니다. 어차피 최적의 상태로 파라미터를 돌려 주는데 굳이 파라미터를 저장하는 checkpoint_cb를 함께 써야 하나 싶어 빼고 돌려 봤는데, 특별히 문제가 발견되지는 않았습니다.
1
2
print(early_stopping_cb.stopped_epoch)
=>9
early_stopping_cb.stopped_epoch에는 조기종료 되었을 때의 epoch가 저장되어 있습니다. 즉, 9번째에 조기종료 되었으니 9번째에 2회 연속으로 손실함수 값이 개선되지 않았고, 7회 때가 최적의 모델이었음을 알 수 있습니다. 손실 곡선을 그려 알아봅시다.
1
2
3
4
5
6
plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
plt.xlabel('epoch')
plt.ylabel('loss')
plt.legend(['train', 'val'])
plt.show()
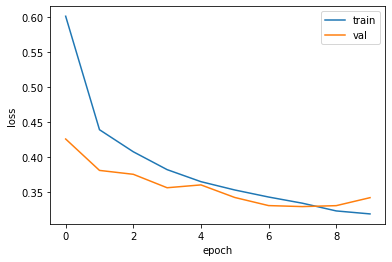
8번째부터 검증 세트의 손실 곡선이 올라가고 있음을 확인하였습니다.
1
2
3
model.evaluate(val_scaled, val_target)
=>375/375 [==============================] - 1s 3ms/step - loss: 0.3291 - accuracy: 0.8832
[0.3291053771972656, 0.8831666707992554]
따라서 모델은 7번째 epoch를 수행했을 때의 모델이며, evaluate로 확인해 보았을 때 곡선의 7번째 epoch와 같은 값을 가짐을 알 수 있습니다.
공부한 내용의 전체 코드는 github에 작성해 두었습니다.