이번 장에서는 차원 축소의 보편적인 방법인 PCA에 관해서 배웠습니다. 원리에 관해서는 선형대수 시간에 배웠던 것이 얼핏 떠오르기는 하는데 제대로 이해하려면 다시 책을 펼쳐봐야 할 것 같습니다.(자그마치 3년 전에 들었던 강의…) 따라서 이번 포스팅에서는 혼공머신러닝 책에서 배운 내용 위주로 코드를 쭉 정리하고, 다음 번 포스팅에서 이번에 다루지 못했던 내용을 공부해 작성하겠습니다.
1. PCA 변환기 사용하기
1
2
3
4
5
6
!wget https://bit.ly/fruits_300_data -O fruits_300.npy
import numpy as np
fruits = np.load('fruits_300.npy')
fruits_2d = fruits.reshape(-1, 100*100)
우선 과일 데이터를 불러옵니다.
1
2
3
4
from sklearn.decomposition import PCA
pca = PCA(n_components=50) # 주성분을 50개로
pca.fit(fruits_2d)
여타 변환기와 마찬가지로, 사용법은 fit한 후 transform하면 됩니다. 이때, n_components는 주성분의 개수를 정하는 것으로, 여기서는 우선 50개로 정하였습니다.
1
2
print(pca.components_.shape)
=>(50, 10000)
PCA가 찾은 주성분의 형태를 출력해보면 50, 10000으로 앞에는 주성분의 개수가, 뒤에는 특성의 개수가 할당됩니다.
1
draw_fruits(pca.components_.reshape(-1, 100, 100)) # 주성분(또는 어떤 특성을 잡아낸 것)
찾아낸 주성분을 reshape해 사진으로 출력해 볼 수도 있는데, 이것은 PCA가 찾아낸 과일의 어떤 특징이라고 볼 수 있습니다.
1
2
3
4
5
6
7
print(fruits_2d.shape)
=>(300, 10000)
fruits_pca = pca.transform(fruits_2d)
print(fruits_pca.shape) # 특성이 50개로 줄음
=>(300, 50)
이처럼 transform 메서드를 사용해 데이터를 변환할 경우 10000개의 특성이 50개로 줄어들게 됩니다. 그렇다면 줄어들은 특성을 다시 원래대로 복구할 수 있을까요?
2. PCA inverse_transform
inverse_transform 메서드는 차원을 축소한 데이터를 다시 원래대로 복구해줍니다.
1
2
3
4
5
6
7
8
9
fruits_inverse = pca.inverse_transform(fruits_pca)
print(fruits_inverse.shape)
=>(300, 10000)
fruits_reconstruct = fruits_inverse.reshape(-1, 100, 100)
for start in [0, 100, 200]: # 100개씩 그림
draw_fruits(fruits_reconstruct[start:start+100])
print("\n")



100%를 다 복구할 수는 없지만, 대부분 충분히 알아볼 수 있는 형태로 복구되었음을 확인하였습니다.
이런 일이 가능한 이유를 살펴봅시다.
1
2
print(np.sum(pca.explained_variance_ratio_))
=>0.921572977651729
각 주성분은 분산을 가장 잘 설명할 수 있는 방향으로 정해지며, 이들이 얼만큼의 분산을 설명하고 있는지를 수치로 알 수 있습니다. 이 수치를 모두 더한 것이 0.92라는 것입니다. 꽤 높은 수치라고 볼 수 있겠습니다. 이제 각 주성분이 설명하고 있는 분산이 어떠한지를 그래프를 그려 알아봅시다.
1
plt.plot(pca.explained_variance_ratio_) # 10번째 주성분 이후로는 큰 의미가 없음
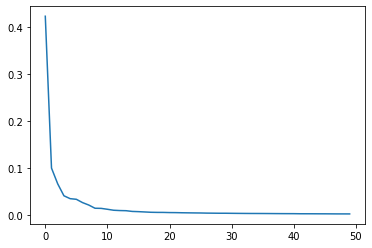
10번째 이후로는 분산을 거의 설명하지 못하고 있음을 알 수 있습니다.
3. 변환기와 다른 알고리즘 함께 사용하기
(1) 로지스틱 회귀
책에서는 분류 문제를 푸는 방법 중 하나인 로지스틱 회귀를 먼저 사용해 보았습니다.
1
2
3
4
5
from sklearn.linear_model import LogisticRegression
lr = LogisticRegression()
target = np.array([0] * 100 + [1] * 100 + [2] * 100)
로지스틱 회귀는 지도 학습 알고리즘이므로 타겟값을 따로 만들어 넣어주어야 합니다.
1
2
3
4
5
6
7
from sklearn.model_selection import cross_validate
scores = cross_validate(lr, fruits_2d, target)
print(np.mean(scores['test_score']))
print(np.mean(scores['fit_time']))
=>0.9966666666666667
=>1.9695783138275147
교차 검증을 해본 결과 꽤 좋은 결과가 나왔습니다. 이번에는 pca로 변환한 것을 넣어봅시다.
1
2
3
4
5
scores = cross_validate(lr, fruits_pca, target)
print(np.mean(scores['test_score']))
print(np.mean(scores['fit_time']))
=>1.0
=>0.05859050750732422
오히려 더 좋은 결과가 나왔습니다. 아마 과대적합되지 않았기 때문이 아닐까 하는 생각이 듭니다. 물론, 계산할 양이 크게 줄었으므로 걸린 시간도 크게 줄었습니다. 여기서 차원을 더 줄여 보면 어떨까요?
1
2
3
4
5
pca = PCA(n_components=0.5) # 주성분분석의 분산의 합이 0.5가 될 때까지
pca.fit(fruits_2d)
print(pca.n_components_)
=>2
n_components에 1 미만의 값을 넣으면 아까 확인했었던 설명된 분산 explained_variance_ratio_의 합이 0.5가 되도록 주성분의 개수를 정합니다. 0.5로 설정하였더니 2개가 되었습니다.
1
2
3
4
5
6
7
8
9
fruits_pca = pca.transform(fruits_2d)
print(fruits_pca.shape)
=>(300, 2)
scores = cross_validate(lr, fruits_pca, target)
print(np.mean(scores['test_score']))
print(np.mean(scores['fit_time']))
=>0.9933333333333334
=>0.04620580673217774
주성분을 2개까지 줄였음에도 교차검증의 score는 크게 떨어지지 않고 좋은 결과가 나왔습니다. 또한, 특성이 50개일 때와 비교해 엄청난 차이는 아니지만 fit_time도 줄었습니다. 책에서는 이 부분이 오히려 늘어나 왜 이런 결과가 나왔는지 궁금했는데, 제 경우에는 줄어들었으니 우선 넘어가보겠습니다.
(2) k-means
두번째로는 저번 시간에 사용했던 k-means 알고리즘을 사용했습니다.
1
2
3
4
5
6
7
from sklearn.cluster import KMeans
km = KMeans(n_clusters=3, random_state=42)
km.fit(fruits_pca)
print(np.unique(km.labels_, return_counts=True)) # 6-2에서 k-means을 사용했던 결과와 거의 비슷
=>(array([0, 1, 2], dtype=int32), array([110, 99, 91]))
결과는 0번 클러스터에 110개, 1번에 99개, 2번에 91개가 할당되었고 6-2에서 차원 축소를 적용하지 않은 데이터를 사용했을 때의 결과와 거의 유사합니다.
4. 차원의 개수가 2개 이하일 때
우리가 일반적으로 좌표평면 또는 산점도를 그려 데이터를 분석하기 위해서는 축이 2개여야 하는데, 이런 이유로 차원의 개수가 2개 이하일 때는 데이터 시각화가 무척 쉬워집니다.
1
2
3
4
5
for label in range(0, 3):
data = fruits_pca[km.labels_ == label]
plt.scatter(data[:,0], data[:,1])
plt.legend(['apple', 'banana', 'pineapple'])
plt.show()
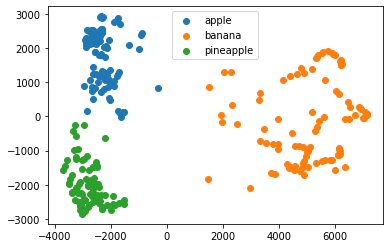
이 데이터를 시각화해보면 2개의 차원만으로도 이미 군집이 충분히 잘 형성되어 있음을 알 수 있습니다. 또한, 모델이 계속 사과와 파인애플을 혼동했던 것이 사과와 파인애플의 결정 경계가 무척 좁기 때문임도 확인해볼 수 있었습니다.
공부한 내용의 전체 코드는 github에 작성해 두었습니다.