이번 장에서는 비정형 데이터를 처음 다루게 되는데, 그 중에서도 사진 데이터를 분류합니다. 우선, 데이터를 준비해 봅시다.
1. 데이터 확인
1
2
3
4
!wget https://bit.ly/fruits_300_data -O fruits_300.npy # !:리눅스 셀 명령어 wget:원격 주소에서 데이터 다운로드
import numpy as np
import matplotlib.pyplot as plt
fruits = np.load('fruits_300.npy')
colab 셀에 !를 앞에 붙이면 리눅스 셀 명령어로 인식하며, wget은 원격 주소에서 데이터를 다운로드합니다. 이 데이터는 캐글에서 제공하는 오픈 데이터이며, 다운로드 받은 후에는 numpy의 load 명령어로 데이터를 불러올 수 있습니다.
1
2
print(fruits.shape)
=>(300, 100, 100)
이 데이터는 총 100 x 100 픽셀의 사진 데이터 300장으로 구성되어 있으며, 100장의 사과, 100장의 파인애플, 100장의 바나나를 담고 있습니다. 시험 삼아 첫 번째 데이터를 살펴봅시다.
1
2
plt.imshow(fruits[0], cmap='gray') # 반전된 상태의 이미지
plt.show()

출력된 이미지는 흰색과 검은색이 반전된 상태로, 이런 처리를 하는 까닭은 기본적으로 연산을 하기 때문에 높은 값일수록 더 중요해지는데, 흰색은 256의 값을 가지고 있어 우리에게 별 의미 없는 배경인데도 불구하고 중요하게 생각되기 때문입니다. 그러나 눈으로 확인할 때는 다시 반전하는 것이 보기에 편하므로 cmap=’gray_r’로 설정하도록 합시다.
1
2
3
4
fig, axs = plt.subplots(1, 2) # 그래프 두 개를 한 번에 출력
axs[0].imshow(fruits[100], cmap='gray_r') # 파인애플
axs[1].imshow(fruits[200], cmap='gray_r') # 바나나
plt.show()
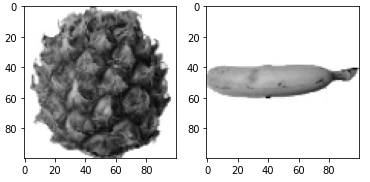
그래프 두 개를 한 번에 출력하고자 할 때는 subplot을 사용하면 되는데, (a, b)의 a는 아래로, b는 오른쪽으로 그래프를 추가합니다.
2. 이미지 별 평균
이제 계산하기 편하도록 100X100 형태의 픽셀을 1X10000으로 재배열합시다.
1
2
3
4
# 각 이미지(100x100)을 1x10000으로 만들기
apple = fruits[0:100].reshape(-1, 100*100)
pineapple = fruits[100:200].reshape(-1, 100*100)
banana = fruits[200:300].reshape(-1, 100*100)
이전에 배웠던 reshape에 (-1, 100*100)을 할당하는 것은 이 경우 (100, 10000)을 할당하는 것과 같습니다. 10000셀을 가진 이미지가 각 100장씩 있기 때문입니다.
이제 각 이미지 별 평균을 계산해 봅시다. axis=1로 설정하면 행 별로 평균을 계산하기 때문에 각 이미지 별 평균을 알 수 있습니다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
print(apple.mean(axis=1)) # 각 이미지의 평균값 계산
=>[ 88.3346 97.9249 87.3709 98.3703 92.8705 82.6439 94.4244 95.5999
90.681 81.6226 87.0578 95.0745 93.8416 87.017 97.5078 87.2019
88.9827 100.9158 92.7823 100.9184 104.9854 88.674 99.5643 97.2495
94.1179 92.1935 95.1671 93.3322 102.8967 94.6695 90.5285 89.0744
97.7641 97.2938 100.7564 90.5236 100.2542 85.8452 96.4615 97.1492
90.711 102.3193 87.1629 89.8751 86.7327 86.3991 95.2865 89.1709
96.8163 91.6604 96.1065 99.6829 94.9718 87.4812 89.2596 89.5268
93.799 97.3983 87.151 97.825 103.22 94.4239 83.6657 83.5159
102.8453 87.0379 91.2742 100.4848 93.8388 90.8568 97.4616 97.5022
82.446 87.1789 96.9206 90.3135 90.565 97.6538 98.0919 93.6252
87.3867 84.7073 89.1135 86.7646 88.7301 86.643 96.7323 97.2604
81.9424 87.1687 97.2066 83.4712 95.9781 91.8096 98.4086 100.7823
101.556 100.7027 91.6098 88.8976]
이렇게만 봐서는 알아보기가 어렵기때문에 히스토그램으로 표시해 봅시다.
1
2
3
4
5
plt.hist(np.mean(apple, axis=1), alpha=0.8) # alpha:투명도 조절
plt.hist(np.mean(pineapple, axis=1), alpha=0.8)
plt.hist(np.mean(banana, axis=1), alpha=0.8)
plt.legend(['apple', 'pineapple', 'banana'])
plt.show()
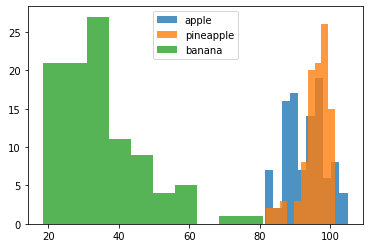
바나나의 평균이 상대적으로 작은 쪽에 위치해 있음을 볼 수 있습니다. 그러나 이것만으로 사과와 파인애플을 구분하기는 어렵습니다.
3. 픽셀 별 평균
그러니 각 픽셀 별 평균을 계산해 봅시다. 이번에는 axis=0으로 설정하여 열별 평균을 계산하면 됩니다.
1
2
3
4
5
6
# 각 픽셀별로 평균 계산
fig, axs = plt.subplots(1, 3, figsize=(20, 5))
axs[0].bar(range(10000), np.mean(apple, axis=0))
axs[1].bar(range(10000), np.mean(pineapple, axis=0))
axs[2].bar(range(10000), np.mean(banana, axis=0))
plt.show()
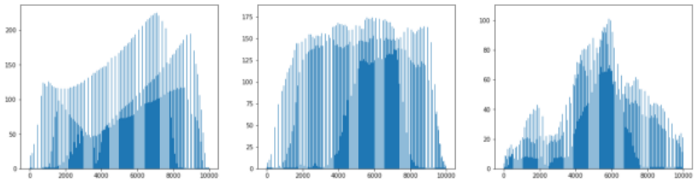
세 과일 모두 다른 경향성을 띠고 있습니다. 이 10000개의 픽셀들을 다시 100x100으로 바꿔 평균 이미지를 그려봅시다.
1
2
3
4
5
6
7
8
9
10
# 10000개의 픽셀을 100x100으로 변형
apple_mean = np.mean(apple, axis=0).reshape(100, 100)
pineapple_mean = np.mean(pineapple, axis=0).reshape(100, 100)
banana_mean = np.mean(banana, axis=0).reshape(100, 100)
# 사과, 파인애플, 바나나의 평균 이미지 그리기
fig, axs = plt.subplots(1, 3, figsize=(20, 5))
axs[0].imshow(apple_mean, cmap='gray_r')
axs[1].imshow(pineapple_mean, cmap='gray_r')
axs[2].imshow(banana_mean, cmap='gray_r')
plt.show()

이제 이렇게 구한 각 픽셀 별 평균을 각 이미지에서 빼고 절댓값을 씌워 절댓값 오차를 계산합시다.
1
2
abs_diff = np.abs(fruits - apple_mean) # 절댓값 오차 계산
abs_mean = np.mean(abs_diff, axis=(1,2)) # 한 이미지 당 절댓값 오차의 평균
이 절댓값 오차가 가장 작은 것부터 순서대로 찾아 주는 함수는 numpy의 argsort입니다. 사과는 총 100개가 있었으므로 순서대로 100개까지 출력해봅시다. subplot을 사용해 행 10개, 열 10개로 100개의 사진을 출력하겠습니다.
1
2
3
4
5
6
7
apple_index = np.argsort(abs_mean)[:100] # 한 이미지 당 절댓값 오차의 평균이 작은 것부터 100개의 index 저장
fig, axs = plt.subplots(10, 10, figsize=(10,10)) # 10 x 10으로 100개의 이미지 출력
for i in range(10):
for j in range(10):
axs[i, j].imshow(fruits[apple_index[i*10 + j]], cmap='gray_r')
axs[i, j].axis('off')
plt.show()

100개의 사과가 잘 출력되었습니다. 그렇다면 바나나는 어떨까요?
1
2
3
4
5
6
7
8
9
10
abs_diff = np.abs(fruits - banana_mean)
abs_mean = np.mean(abs_diff, axis=(1,2))
banana_index = np.argsort(abs_mean)[:100]
fig, axs = plt.subplots(10, 10, figsize=(10,10))
for i in range(10):
for j in range(10):
axs[i, j].imshow(fruits[banana_index[i*10 + j]], cmap='gray_r')
axs[i, j].axis('off')
plt.show()

98개의 바나나를 찾았지만, 두 개의 사과가 바나나 클러스터에 포함되었습니다.
공부한 내용의 전체 코드는 github에 작성해 두었습니다.
https://github.com/ynkim0/study/blob/main/6-1.ipynb