이 책에서 결정 트리를 소개한 것은 로지스틱 회귀와 대비하여, 로지스틱 회귀의 훈련된 coef_와 intercept_ 값이 무엇인지는 볼 수 있어도 왜 그런 값을 도출하는지는 설명하기 어렵다는 점에 있었습니다. 결정 트리의 장점은 무엇을 기준으로 모델을 분류하는지 직관적으로 알 수 있다는 것입니다. 이제 우리는 결정 트리의 형태, 원리와 규제에 관해 알아보겠습니다.
1. 결정 트리의 형태
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
import pandas as pd
wine = pd.read_csv('https://bit.ly/wine_csv_data')
data = wine[['alcohol', 'sugar', 'pH']].to_numpy()
target = wine['class'].to_numpy()
from sklearn.model_selection import train_test_split
train_input, test_input, train_target, test_target = train_test_split(
data, target, test_size=0.2, random_state=42) # test_size의 기본값은 0.25이지만 데이터의 크기가 충분히 크므로 20%만 분리
from sklearn.preprocessing import StandardScaler
ss = StandardScaler()
ss.fit(train_input)
train_scaled = ss.transform(train_input)
test_scaled = ss.transform(test_input)
from sklearn.tree import DecisionTreeClassifier # 결정트리
dt = DecisionTreeClassifier(random_state=42)
dt.fit(train_scaled, train_target)
print(dt.score(train_scaled, train_target)) # 과대적합
print(dt.score(test_scaled, test_target))
=>0.996921300750433
=>0.8592307692307692
데이터를 준비하고 결정 트리로 모델을 훈련시킵니다. 평가 결과 이 모델은 명백히 과대적합 되어있음을 알 수 있습니다.
우선 matplotlib.pyplot과 sklearn_tree의 plot_tree를 import해 훈련된 트리가 어떤 형태인지 확인해봅시다.
1
2
3
4
5
6
import matplotlib.pyplot as plt
from sklearn.tree import plot_tree
plt.figure(figsize=(10,7)) # 그래프의 크기 설정
plot_tree(dt)
plt.show()
굉장히 복잡한 트리가 출력되었기 때문에 이를 좀 더 쉽게 알아보기 위해 깊이가 1인 노드까지만 출력해 봅시다.
1
2
3
plt.figure(figsize=(10,7))
plot_tree(dt, max_depth=1, filled=True, feature_names=['alcohol', 'sugar', 'pH']) # 트리의 깊이를 1까지만 보여줌, filled : 양성 클래스와 음성 클래스의 비율을 색으로 표시
plt.show()
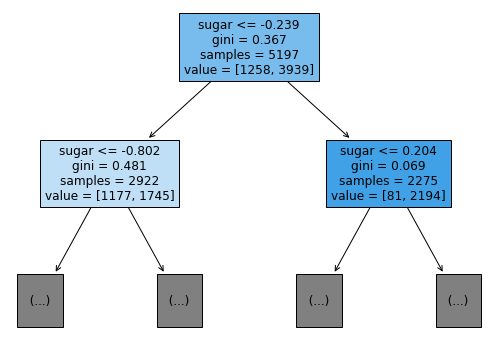
filled는 양성 클래스와 음성 클래스의 비율을 색으로 표시하여 직관적으로 알 수 있게 해주며, feature_name에 특성을 전달하면 위의 트리와 같이 각 노드에 기준이 되는 특성을 표시해주므로 알아보기가 더 쉽습니다.
2. 결정 트리의 원리
루트 노드를 보면 데이터는 sugar이 -0.239보다 작음을 만족시키면 왼쪽 자식으로, 그렇지 않으면 오른쪽 자식으로 이동하고 있습니다. 이 -0.239라는 수치를 이해하기 위해서는 지니 불순도를 이해해야 합니다.
지니 불순도 = 1 — (음성 클래스 비율² + 양성 클래스 비율²)
이것의 의미는 두 클래스의 비율이 절반씩, 즉 1/2씩일 때와 한 클래스가 100%를 차지하고 있을 때를 각각 넣어보면 이해하기 조금 더 쉽습니다. 절반씩일때는 1/2, 100%일 때는 0이 됩니다. 즉, 두 클래스의 비율이 절반에 가까울 때 가장 높은 불순도, 100%에 가까울 때 가장 낮은 불순도를 가지고 있다고 말할 수 있겠습니다. 한 노드에 속한 샘플의 클래스가 반반씩이라면, 모델은 그것이 무엇인지 예측할 수 없을 테고 100%라면 확신할 수 있을 것이니, 저는 지니 불순도를 ‘얼마나 분류하기 쉽느냐’를 나타내는 수치로 이해하였습니다.
그렇다면, 트리가 부모 노드에서 두 자식 노드로 분화할 때 이 자식들 쪽의 불순도가 더 적고, 그 차이가 더 많이 날수록 더 큰 효과를 낳게 될 것입니다. 이 불순도의 차이는 정보 이득이라고 부르며, 다음과 같이 계산합니다.
정보 이득 = 부모의 불순도 — (왼쪽 노드 샘플 수/부모의 샘플 수) x 왼쪽 노드 불순도 — (오른쪽 노드 샘플 수/부모의 샘풀 수) x 오른쪽 노드 불순도
더 많은 샘플이 속해 있는 노드일수록 지니 불순도가 분류하는 샘플도 많아질테니 부모 노드에서 얼마나 많은 샘플이 자식 노드로 넘어오는지를 곱해 주는 것입니다.
다시 본론으로 돌아와서, 결정 트리는 이 정보 이득이 최대가 되도록 기준을 정합니다.
3. 결정 트리의 규제
이제 결정 트리가 어떻게 동작하는지에 관해 알았으니, 앞선 과대적합을 해결하는 법에 관해 알아봅시다. 결정 트리에서는 이 작업을 가지치기라고 합니다. 모델을 만들 때에 우리는 max_depth라는 파라미터를 설정할 수 있는데, 이것은 트리의 최대 깊이를 제한해 모델을 단순화합니다.
1
2
3
4
5
6
7
dt = DecisionTreeClassifier(max_depth=3, random_state=42) # max_depth를 줄이면 모델을 더 간단하게 만들어 과대적합을 방지
dt.fit(train_scaled, train_target)
print(dt.score(train_scaled, train_target))
print(dt.score(test_scaled, test_target))
=>0.8454877814123533
=>0.8415384615384616
훈련 세트의 평가 점수는 낮아졌지만 테스트 세트의 평가 점수는 비슷한 상황임을 볼 수 있습니다. 이 모델이 어떻게 동작하고 있는지 다시 트리를 그려 봅시다.
1
2
3
plt.figure(figsize=(20,15))
plot_tree(dt, filled=True, feature_names=['alcohol', 'sugar', 'pH'])
plt.show()
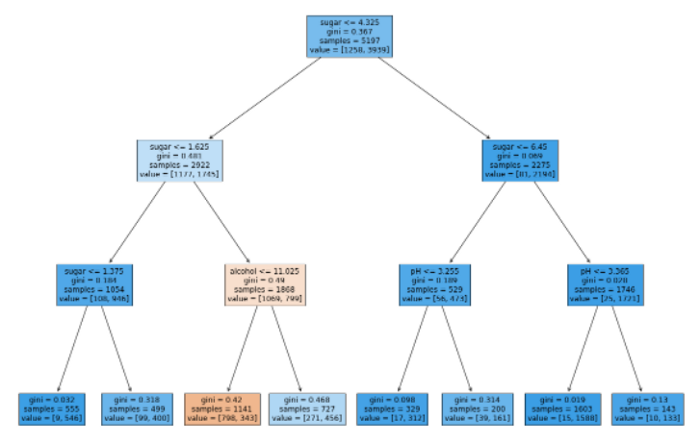
깊이 3인 노드 중 3번째 리프 노드만이 레드와인으로 분류됨을 확인하였습니다.
결정 트리는 정보 이득을 계산하기 때문에 어떤 특성이 중요한지도 직접 눈으로 볼 수 있게 해줍니다.
1
2
print(dt.feature_importances_) # 각 특성의 중요도를 확인 가능
=>[0.12345626 0.86862934 0.0079144 ]
두 번째 특성인 당도가 가장 중요한 특성이라는 것을 알 수 있습니다.
마지막으로, 가지 치기 방법에는 깊이를 조정하는 것만이 있는 것은 아닙니다. 전체에 관해 해당 노드의 정보 이득이 일정 상수 이하일 때, 더이상 자식을 만들지 않도록 하는 min_impurity_decrease를 설정할 수도 있습니다.
1
2
3
4
5
6
7
dt = DecisionTreeClassifier(min_impurity_decrease=0.0005, random_state=42) # min_impurity_decrease < 정보 이득 x 노드의 샘플 수 / 전체 샘플 수이면 더이상 작동하지 않음, 가지치기의 다른 방법
dt.fit(train_input, train_target)
print(dt.score(train_input, train_target))
print(dt.score(test_input, test_target))
=>0.8874350586877044
=>0.8615384615384616
이것은 이전에 max_depth로 가지치기 했던 것보다 조금 더 높은 성능을 보여줍니다.
공부한 내용의 전체 코드는 github에 작성해 두었습니다.