최근접 이웃 분류에 관해 말하기에 앞서, 데이터를 준비합시다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
import pandas as pd
fish = pd.read_csv('https://bit.ly/fish_csv_data')
fish.head() # 앞에 있는 다섯 개의 데이터 보여줌
fish_input = fish[['Weight','Length','Diagonal','Height','Width']].to_numpy() # Species 열을 제외한 모든 열을 numpy 배열로 바꿔 저장
fish_target = fish['Species'].to_numpy() # Species 열은 타겟
from sklearn.model_selection import train_test_split # 훈련 세트와 테스트 세트 분리
train_input, test_input, train_target, test_target = train_test_split(
fish_input, fish_target, random_state=42)
from sklearn.preprocessing import StandardScaler # 표준화
ss = StandardScaler()
ss.fit(train_input)
train_scaled = ss.transform(train_input)
test_scaled = ss.transform(test_input)
데이터의 형태는 다음과 같습니다.
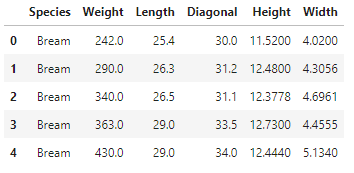
1. k-최근접 이웃 분류기
k-최근접 이웃 분류 문제를 공부했을 때 이 알고리즘은 이진 분류 문제에 적절한 것 같다고 생각한 적이 있습니다. 그런데, 그 생각이 틀렸다는 것을 이번 장에서 알 수 있었습니다. 저는 단순히 각 class에 0, 1, 2와 같은 숫자를 넣어 어느 쪽에 가까운지를 숫자 하나로 표시하는 것을 생각했었지만, 실제 다중 분류 문제에서 이 알고리즘은 예측 확률을 배열 형태로 표시하여 모든 class에 관한 확률을 표시했습니다.
1
2
3
4
5
6
7
8
9
from sklearn.neighbors import KNeighborsClassifier # k-최근접 이웃 분류
kn = KNeighborsClassifier(n_neighbors=3)
kn.fit(train_scaled, train_target)
print(kn.score(train_scaled, train_target))
print(kn.score(test_scaled, test_target))
=>0.8907563025210085
=>0.85
그리 높은 정확도를 보여주고 있지는 않지만, 이 알고리즘으로도 다중 분류 문제를 풀 수 있다는 것입니다. 예측 확률을 확인하기 위해서는 predict_proba 명령어를 사용합니다. 앞에 있는 다섯 개의 데이터를 예측해보고, 예측 확률을 확인해봅시다.
1
2
3
4
5
6
7
8
9
10
11
print(kn.predict(test_scaled[:5]))
=>['Perch' 'Smelt' 'Pike' 'Perch' 'Perch']
import numpy as np
proba = kn.predict_proba(test_scaled[:5]) # predict_proba : 각 클래스들의 예측 확률
print(np.round(proba, decimals=4)) # 소수 넷째 자리에서 반올림
=>[[0. 0. 1. 0. 0. 0. 0. ]
[0. 0. 0. 0. 0. 1. 0. ]
[0. 0. 0. 1. 0. 0. 0. ]
[0. 0. 0.6667 0. 0.3333 0. 0. ]
[0. 0. 0.6667 0. 0.3333 0. 0. ]]
이 class들의 예측 확률이 어떤 순서로 나열되어 있는지는 classes_를 통해 확인할 수 있습니다.
1
2
print(kn.classes_)
=>['Bream' 'Parkki' 'Perch' 'Pike' 'Roach' 'Smelt' 'Whitefish']
네 번째 데이터는 Perch가 0.6667, Pike가 0.3333이므로 옳은 결과인 Perch가 출력되었습니다. 이것을 좀 더 자세히 알아보기 위해, 네 번째 데이터의 이웃을 살펴봅시다.
1
2
3
4
distances, indexes = kn.kneighbors(test_scaled[3:4]) # 2차원 배열을 가져오기 위해 슬라이싱을 사용했음
print(train_target[indexes]) # 4번째 데이터의 이웃 확인
=>[['Roach' 'Perch' 'Perch']]
Perch 둘, Roach 하나로 각각 2/3, 1/3의 확률이 잘 계산
Perch 둘, Roach 하나로 각각 2/3, 1/3의 확률이 잘 계산되었음을 알 수 있습니다. 그러나 neighbors=3인 경우 확률은 0, 1/3, 2/3, 1만이 나올 수 있으며 이 결과는 매우 제한적이므로 좀 더 복잡한 모델을 도입합시다.
2. 로지스틱 회귀
로지스틱 회귀는 앞서 배웠던 선형 회귀처럼 특성 앞에 계수를 곱하고 절편을 더하는 선형 방정식을 사용합니다. 방정식의 결과값, z는 음수 또는 양수를 도출하는데 우리는 이것을 확률로 이용하기 위해서, 1/(1+exp^(-z))라는 시그모이드 함수에 z를 대입하여 0과 1 사이의 값으로 만들어 줍니다. 시그모이드 함수는 음수는 0.5 이하의 값으로, 양수는 0.5 이상의 값으로 변환하며, 사이킷런에서는 0.5일 경우 음수로 판단합니다. 아래 그래프는 시그모이드 함수입니다.
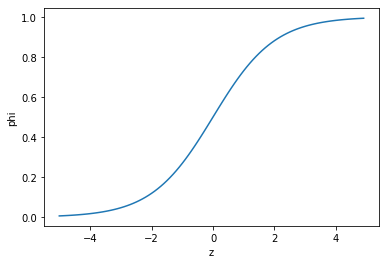
(1) 이중 분류
로지스틱 회귀로 다중 분류를 하기 전에, 이 책에서는 이중 분류를 먼저 소개하기 때문에 우리는 데이터를 가공할 필요가 있습니다.
1
2
3
4
# 타겟 값이 도미이거나 빙어인 데이터만 저장
bream_smelt_indexes = (train_target == 'Bream') | (train_target == 'Smelt')
train_bream_smelt = train_scaled[bream_smelt_indexes]
target_bream_smelt = train_target[bream_smelt_indexes]
bream_smelt_indexes는 데이터의 타겟 값이 Bream이거나 Smelt일 경우에는 true, 그렇지 않을 경우에는 false가 되며 배열의 index 자리에 매개변수로 들어갔을 경우 배열의 원소 개수만큼 [true, false, true, …]와 같은 배열의 형태로 전달되어 불리언 인덱싱을 하게 됩니다. 이제 train_bream_smelt에는 타겟 값이 도미이거나 빙어인 데이터만 있으니, 이진 분류를 수행해 봅시다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
from sklearn.linear_model import LogisticRegression # 로지스틱 회귀(분류 문제에 사용)
lr = LogisticRegression()
lr.fit(train_bream_smelt, target_bream_smelt) # 이진 분류
print(lr.predict(train_bream_smelt[:5])) # 앞 다섯 개의 값 예측
=>['Bream' 'Smelt' 'Bream' 'Bream' 'Bream']
print(lr.predict_proba(train_bream_smelt[:5])) # 음성 클래스(0)의 확률, 양성 클래스(1)의 확률
=>[[0.99759855 0.00240145]
[0.02735183 0.97264817]
[0.99486072 0.00513928]
[0.98584202 0.01415798]
[0.99767269 0.00232731]]
print(lr.classes_) # Bream이 음성 클래스, Smelt가 양성 클래스
=>['Bream' 'Smelt']
이처럼 로지스틱 회귀는 음성 클래스의 확률과 양성 클래스의 확률 중 더 높은 쪽의 확률을 택하여 예측치로 출력하며, 어떤 것이 음성 클래스이고 어떤 것이 양성 클래스인지는 classes_를 확인하면 알 수 있습니다.
1
2
3
4
5
6
7
decisions = lr.decision_function(train_bream_smelt[:5]) # decision_function : z값
print(decisions)
=>[-6.02927744 3.57123907 -5.26568906 -4.24321775 -6.0607117 ]
from scipy.special import expit # 시그모이드 함수
print(expit(decisions))
=>[0.00240145 0.97264817 0.00513928 0.01415798 0.00232731]
또, 아까 z값을 시그모이드 함수에 대입해 예측 확률을 계산한다고 했는데, decisions_function으로 얻은 z값에 직접 시그모이드 함수를 씌워 보면 predict_proba와 같은 값이 나오는 것을 확인하였습니다.
(2) 다중 분류
이제 다중 분류를 수행해봅시다. 다중 분류에서는 시그모이드 함수 대신 softmax 함수를 사용합니다. softmax 함수는 모든 class의 확률을 더해 1이 되도록 만들어주는 함수입니다. 각각을 0~1 사이의 값으로 만들어주는 시그모이드를 그대로 사용한다면 표본공간의 모든 배반사건의 합이 1이라는 공리적 확률에 어긋나므로, 시그모이드를 사용할 수는 없습니다.
하지만 우리 눈에는 어떤 함수를 쓰는지까지 보이지는 않으므로 과정 자체는 이진 분류와 동일합니다.
1
2
3
4
5
lr = LogisticRegression(C=20, max_iter=1000) # max_iter : 반복 횟수
lr.fit(train_scaled, train_target)
print(lr.score(train_scaled, train_target))
print(lr.score(test_scaled, test_target))
훈련 평가는 0.9327731092436975, 테스트 평가는 0.925를 기록했으며 softmax 함수는 시그모이드 함수의 위치와 같은 scipy.special에서 softmax를 import하면 된다는 점까지 알아두고 다음 장으로 넘어갑시다.
공부한 내용의 전체 코드는 github에 작성해 두었습니다.