k-최근접 이웃 회귀는 예측하고자 하는 데이터가 훈련 세트의 범위를 벗어난 경우 제대로 된 예측을 하지 못한다는 문제점이 있습니다. 따라서 이전까지 훈련 세트의 농어 길이 최대치가 45 안팎이었으므로, 길이 50의 농어나 길이 100의 농어를 예측하고자 해도 근처의 데이터가 45 이전의 데이터이므로 그것들의 평균치를 예측치로 갖게 됩니다.
이 때문에 이번 장에서는 새로운 알고리즘인 선형 회귀와 다항 회귀에 관해 배웠습니다.
1. 선형 회귀
선형 회귀란 훈련 세트에 적합하도록 y=ax+b의 형태를 갖는 직선의 a와 b값을 찾도록 훈련시켜 이것을 가지고 예측하는 것입니다. 사이킷런에서 해당 패키지를 불러와 사용할 수 있기 때문에 코드 자체는 어렵지 않습니다.
1
2
3
4
5
6
from sklearn.linear_model import LinearRegression # 선형 회귀
lr = LinearRegression()
# 선형 회귀 모델 훈련
lr.fit(train_input, train_target)
# 50cm 농어에 대한 예측
print(lr.predict([[50]]))
이것은 길이가 50, 무게가 150인 농어에 관해 1033.33333333의 예측치를 내놓았던 k-최근접 회귀보다 조금 더 정확한 값인 1241.83860323를 도출하였습니다.
훈련된 모델의 기울기인 a와 y절편 b는 coef_와 intercept_에 저장되어 있으므로 확인해볼 수 있습니다.
1
2
print(lr.coef_, lr.intercept_)
=>[39.01714496] -709.0186449535477
이 선형 모델은 k-최근접 이웃 회귀보다는 정확도가 높지만, 막상 정확도를 확인해보면 훈련 세트와 테스트 세트 모두 그리 높지 않습니다.
1
2
3
4
print(lr.score(train_input, train_target))
=> 0.939846333997604
print(lr.score(test_input, test_target))
=>0.8247503123313558
훈련 세트의 평가가 테스트 세트보다 높지만, 훈련 세트의 평가 자체도 낮은 편이기 때문에 이것은 과대적합이라기보다는 전체적으로 과소적합 되어있는 것으로 볼 수 있습니다.
2. 다항 회귀
이 문제를 해결하기 위해서 우리는 다항 회귀를 도입합니다. 직선 형태의 모델을 사용했던 선형 회귀와 달리, 다항 회귀를 이용하면 2차, 3차함수의 곡선을 사용할 수 있기 때문에 더 복잡한 모델을 구성할 수 있게 됩니다. 다항 회귀를 사용하는 방법도 어렵지 않습니다. 선형 회귀에 사용한 특성을 제곱하여 나온 새로운 특성을 추가하면 되는 것입니다.
1
2
3
# 특성에 2차 항 추가
train_poly = np.column_stack((train_input ** 2, train_input))
test_poly = np.column_stack((test_input ** 2, test_input))
앞서 공부한 numpy의 column_stack을 이용하면 아주 간편하게 추가할 수 있습니다. 이후의 과정은 선형 회귀와 동일합니다.
훈련시킨 모델(ax²+bx+c)의 a, b, c를 찾아 모델을 그래프로 그려봅시다.
1
2
print(lr.coef_, lr.intercept_)
=>[ 1.01433211 -21.55792498] 116.0502107827827
선형 회귀와 같은 방법으로 a = 1.01433211, b = -21.55792498, c = 116.0502107827827임을 알 수 있습니다.
1
2
3
4
5
6
7
8
9
10
11
# 구간별 직선을 그리기 위해 15에서 49까지 정수 배열을 만듭니다
point = np.arange(15, 50)
# 훈련 세트의 산점도를 그립니다
plt.scatter(train_input, train_target)
# 15에서 49까지 2차 방정식 그래프를 그립니다
plt.plot(point, 1.01*point**2 - 21.6*point + 116.05)
# 50cm 농어 데이터
plt.scatter([50], [1574], marker='^')
plt.xlabel('length')
plt.ylabel('weight')
plt.show()
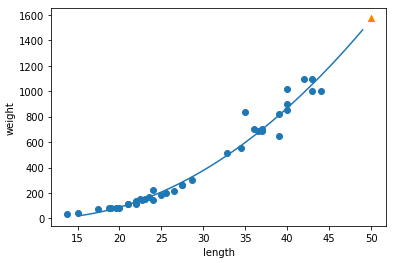
이 모델이 데이터에 꽤 잘 맞는다는 것을 눈으로 확인하였는데, 이제 평가를 통해 확인해봅시다.
1
2
3
4
print(lr.score(train_poly, train_target))
=>0.9706807451768623
print(lr.score(test_poly, test_target))
=>0.9775935108325122
앞서 만든 직선형 모델보다 훨씬 높은 정확도를 보여주지만, 테스트 세트보다 훈련 세트의 정확도가 낮다는 점에서 여전히 약간의 과소 적합이 있음을 알 수 있습니다. 이것의 해결법은 다음 장에서 소개한다고 합니다.
공부한 내용의 전체 코드는 github에 작성해 두었습니다.