이 장에서는 지도학습의 큰 두 분야인 분류와 회귀 문제 중 회귀를 처음으로 다루어 보았습니다. 회귀에 관해서 이야기하기 전에, 새로 배운 numpy 배열의 reshape이라는 기능에 관해 간단히 언급하겠습니다.
1. numpy의 reshape으로 배열 형태 바꾸기
1
2
test_array = np.array([1,2,3,4])
test_array = test_array.reshape(2, 2)
reshape는 배열을 원하는 형태로 바꿔 줍니다. 위와 같이 입력했다면, 2행 2열의 [[1 2] [3 4]]로 변환될 것입니다. 주의할 점은 2 x 2 행렬이라면 전체 원소의 개수가 4개여야 한다는 것입니다. 4개의 원소를 가지고 2 x 3 행렬을 만들 수는 없기 때문입니다. 이 reshape에는 유용한 기능이 한 가지 더 있습니다.
1
train_input = train_input.reshape(-1, 1)
위와 같이 매개변수로 -1을 전달하면, 전체 원소의 개수에 맞춰 올바른 값이 할당됩니다. 이것이 유용한 이유는 전체 원소의 개수를 기억하고 있지 않더라도 쉽게 reshape할 수 있기 때문입니다.
2. 회귀
이제 회귀에 관해 알아볼 시간입니다. 회귀란 여러 개, 또는 한 개의 독립변수를 이용해 종속변수의 값을 예측하는 것입니다. 예를 들어, 이 책에서는 농어의 길이라는 독립변수를 이용해서 농어의 무게라는 종속변수를 예측합니다. 따라서, 회귀를 이용할 수 있는 전제조건은 알고자 하는 것이 어떤 독립변수에 종속적이라는 것입니다. 그것을 알아보기 위해서는 산점도를 그려보면 됩니다.
1
2
3
4
5
import matplotlib.pyplot as plt
plt.scatter(perch_length, perch_weight)
plt.xlabel('length')
plt.ylabel('weight')
plt.show()
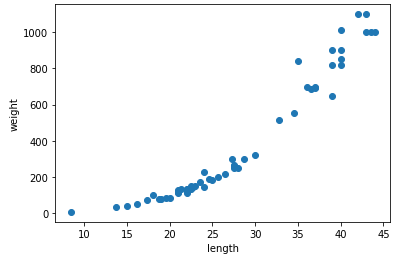
이 산점도를 보면 길이가 길어질수록 농어의 무게 또한 증가하며, 이는 두 변수 사이에 어떤 규칙이 존재하고 있음을 알 수 있습니다.
확인을 마쳤으니, 모델을 훈련시키고 평가해 봅시다. 사용한 알고리즘은 분류때도 사용했던 k-최근접 이웃 회귀로, 분류와의 차이점은 결과 도출에 있습니다. 따로 설정하지 않는다면 기본값인 5개의 근접한 데이터를 찾는 것까지는 같습니다. 분류 때는 이 데이터의 타겟 값들이 1인지 0인지를 찾아 비율을 계산했지만, 회귀에서는 근접한 데이터들의 타겟 값의 평균을 결과로 도출합니다.
1
2
3
4
5
from sklearn.neighbors import KNeighborsRegressor # k-최근접 이웃 회귀
knr = KNeighborsRegressor()
# k-최근접 이웃 회귀 모델을 훈련합니다
knr.fit(train_input, train_target)
knr.score(test_input, test_target)
이 모델은 0.992809406101064의 정확도를 가지고 있습니다. 이 정확도는 결정계수인 R²의 수치입니다. 결정계수는 SSR/SST, 또는 1-SSE/SST로 계산하며 이것이 어떻게 정확도가 될 수 있는지에 관한 이야기는 통계학 시간에 배웠던 기억이 있는데, 이 이야기는 책에서는 자세히 설명되지 않았기 때문에 발표 준비를 하면서 따로 포스팅하겠습니다.
3. 과대적합과 과소적합
다음으로는 과대적합과 과소적합에 관해 알아보겠습니다. 기본적으로 모델은 훈련 세트를 이용해 훈련하기 때문에, 일반적인 경우라면 당연히 훈련 세트로 평가한 정확도가 테스트 세트로 평가한 정확도보다 높게 나와야 합니다. 그런데, 방금 만든 모델의 경우 훈련 세트로 평가하면 0.9698823289099254의 정확도가 나오며 이것은 테스트 세트로 평가한 것보다 낮습니다. 따라서, 이 모델은 과소적합 되어있습니다.
그러므로, 과소적합이란 모델이 훈련 세트에 덜 맞춰져 있는 경우라고 말할 수 있습니다. 반대로, 과대적합이란 모델이 훈련 세트에 지나치게 맞춰져 일반성을 상실한 경우입니다. 훈련 세트는 전체 표본의 경향성을 가지고 있기 때문에 전체 표본을 대표하지만, 그렇다고 해서 전체 표본이 될 수는 없기 때문에 모델은 과소적합 되어서도, 과대적합 되어서도 안 됩니다.
이것을 체감하기 위해서, 다음 예를 살펴봅시다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# k-최근접 이웃 회귀 객체를 만듭니다
knr = KNeighborsRegressor()
# 5에서 45까지 x 좌표를 만듭니다
x = np.arange(5, 45).reshape(-1, 1)
# n = 1, 5, 10일 때 예측 결과를 그래프로 그립니다.
for n in [1, 5, 10]:
# 모델 훈련
knr.n_neighbors = n
knr.fit(train_input, train_target)
# 지정한 범위 x에 대한 예측 구하기
prediction = knr.predict(x)
# 훈련 세트와 예측 결과 그래프 그리기
plt.scatter(train_input, train_target)
plt.plot(x, prediction)
plt.title('n_neighbors = {}'.format(n))
plt.xlabel('length')
plt.ylabel('weight')
plt.show()
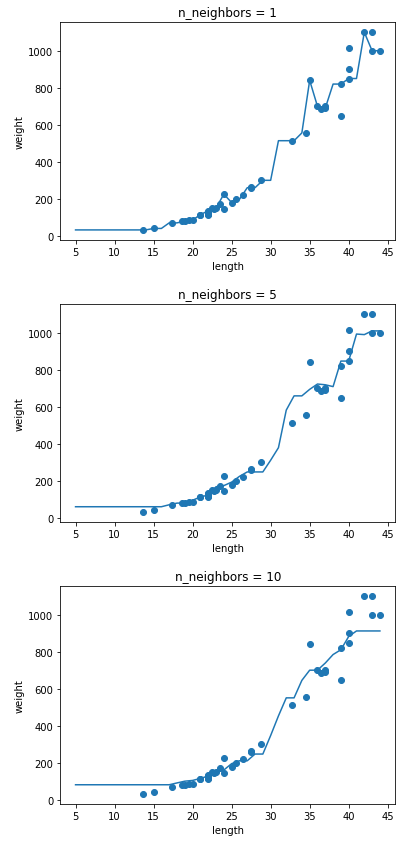
위 그래프는 n_neighbors의 변화에 따른 모델의 예측 그래프를 표시한 것입니다. 해당 변수가 커질수록 모델은 훈련 세트의 세세한 국소적 변화보다는 전체적 경향성을 따르게 됩니다. 책에서는 이 값이 커질수록 모델이 단순해진다고 이야기했습니다.
다시 돌아와서, 기본값인 5에서 모델이 과소적합 되어있음을 발견하였으니 n_neighbors를 3으로 조정해봅시다.
1
2
3
4
5
6
7
8
# 이웃의 갯수를 3으로 설정합니다(과소적합을 해결하기 위해 모델을 더 복잡하게, 즉 국소적인 변화에 더 예민하게 만드는 것)
knr.n_neighbors = 3
# 모델을 다시 훈련합니다
knr.fit(train_input, train_target)
print(knr.score(train_input, train_target))
=> 0.9804899950518966
print(knr.score(test_input, test_target))
=> 0.9746459963987609
이번에는 훈련 세트의 정확도가 더 높아지며 문제가 해결되었습니다. 단순히 모델을 믿는 것이 아니라 하이퍼파라미터의 조정이 꼭 필요하다는 점을 알 수 있었습니다.
공부한 내용의 전체 코드는 github에 작성해 두었습니다.