Home 선형 SVM 분류
Post
Cancel

선형 SVM 분류

By 김예나
Posted 2022-05-03 Updated 2022-05-03 9 min read

혼공머신러닝에서 힌지 손실을 사용하는 모델로 SVM을 소개하였는데, 진도에 여유가 있는 김에 핸즈온 머신러닝 책을 통해 공부해 보았습니다.

1. 결정 경계

핸즈온 머신러닝에서는 SVM 분류 예제로 붓꽃(iris) 데이터셋을 사용합니다. 이 데이터셋의 타겟은 setosa, versicolor, virginica의 세 가지인데, 이진 분류의 수행을 위하여 setosa, versicolor에 관한 데이터를 분리했습니다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14

from sklearn.svm import SVC
from sklearn import datasets

iris = datasets.load_iris()
X = iris["data"][:, (2, 3)]  # 꽃잎 길이, 꽃잎 너비
y = iris["target"]

setosa_or_versicolor = (y == 0) | (y == 1)
X = X[setosa_or_versicolor]
y = y[setosa_or_versicolor]

# SVM 분류 모델
svm_clf = SVC(kernel="linear", C=float("inf"))
svm_clf.fit(X, y)

이 데이터와 몇 가지의 결정 경계를 시각화하여 확인해봅시다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46

# 나쁜 모델
x0 = np.linspace(0, 5.5, 200) # 구간 시작점, 구간 끝점, 구간 내 숫자 개수
pred_1 = 5*x0 - 20
pred_2 = x0 - 1.8
pred_3 = 0.1 * x0 + 0.5

def plot_svc_decision_boundary(svm_clf, xmin, xmax):
    w = svm_clf.coef_[0]
    b = svm_clf.intercept_[0]

    # 결정 경계에서 w0*x0 + w1*x1 + b = 0 이므로
    # => x1 = -w0/w1 * x0 - b/w1
    x0 = np.linspace(xmin, xmax, 200)
    decision_boundary = -w[0]/w[1] * x0 - b/w[1]

    margin = 1/w[1]
    gutter_up = decision_boundary + margin
    gutter_down = decision_boundary - margin

    svs = svm_clf.support_vectors_
    plt.scatter(svs[:, 0], svs[:, 1], s=180, facecolors='#FFAAAA')
    plt.plot(x0, decision_boundary, "k-", linewidth=2)
    plt.plot(x0, gutter_up, "k--", linewidth=2)
    plt.plot(x0, gutter_down, "k--", linewidth=2)

plt.figure(figsize=(12,2.7))

plt.subplot(121)
plt.plot(x0, pred_1, "g--", linewidth=2)
plt.plot(x0, pred_2, "m-", linewidth=2)
plt.plot(x0, pred_3, "r-", linewidth=2)
plt.plot(X[:, 0][y==1], X[:, 1][y==1], "bs", label="Iris-Versicolor")
plt.plot(X[:, 0][y==0], X[:, 1][y==0], "yo", label="Iris-Setosa")
plt.xlabel("length", fontsize=14)
plt.ylabel("width", fontsize=14)
plt.legend(loc="upper left", fontsize=14)
plt.axis([0, 5.5, 0, 2])

plt.subplot(122)
plot_svc_decision_boundary(svm_clf, 0, 5.5)
plt.plot(X[:, 0][y==1], X[:, 1][y==1], "bs")
plt.plot(X[:, 0][y==0], X[:, 1][y==0], "yo")
plt.xlabel("length", fontsize=14)
plt.axis([0, 5.5, 0, 2])

plt.show()

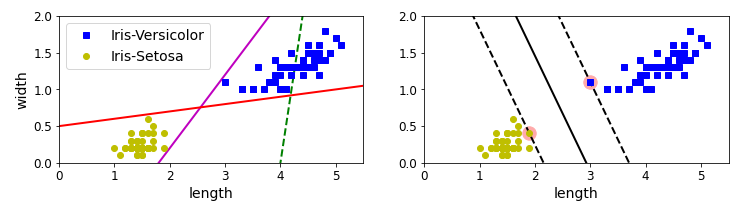
image

왼쪽이 잘못된 결정 경계, 오른쪽이 좋은 결정 경계입니다. 좋은 결정 경계는 두 클래스 사이의 거리가 가장 길게 되도록 합니다. 도로(점선) 밖에 샘플을 추가해도 결정 경계가 변하지 않을 때 도로를 결정하는 두 개의 샘플을 서포트 벡터라고 합니다.

2. 스케일

그간 스케일에 민감한 몇몇 모델들을 다루어 본 적이 있었는데, SVM 또한 스케일에 민감합니다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

Xs = np.array([[1, 50], [5, 20], [3, 80], [5, 60]]).astype(np.float64)
ys = np.array([0, 0, 1, 1])
svm_clf = SVC(kernel="linear", C=100)
svm_clf.fit(Xs, ys)

plt.figure(figsize=(12,3.2))
plt.subplot(121)
plt.plot(Xs[:, 0][ys==1], Xs[:, 1][ys==1], "bo")
plt.plot(Xs[:, 0][ys==0], Xs[:, 1][ys==0], "ms")
plot_svc_decision_boundary(svm_clf, 0, 6)
plt.xlabel("$x_0$", fontsize=20)
plt.ylabel("$x_1$  ", fontsize=20, rotation=0)
plt.title("before scaling", fontsize=16)
plt.axis([0, 6, 0, 90])

from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
X_scaled = scaler.fit_transform(Xs)
svm_clf.fit(X_scaled, ys)

plt.subplot(122)
plt.plot(X_scaled[:, 0][ys==1], X_scaled[:, 1][ys==1], "bo")
plt.plot(X_scaled[:, 0][ys==0], X_scaled[:, 1][ys==0], "ms")
plot_svc_decision_boundary(svm_clf, -2, 2)
plt.xlabel("$x_0$", fontsize=20)
plt.title("after scaling", fontsize=16)
plt.axis([-2, 2, -2, 2])

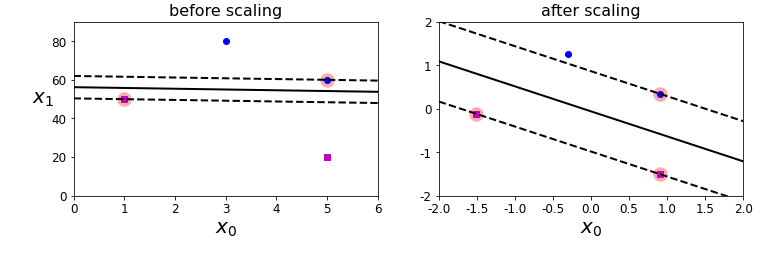
image

왼쪽은 StandardScaler를 사용하지 않았을 때의 결정 경계이고 오른쪽은 사용했을 때의 결정 경계입니다. 사용했을 때 도로의 폭이 넓은 것을 확인할 수 있습니다. 정규화를 하지 않았을 때 결정 경계는 특성 스케일이 큰 축에 거의 수직한 방향으로 결정됩니다. 다른 특성이 결정 경계에 영향을 미치지 못하고 있기 때문입니다.

3. 하드 마진 분류

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

X_outliers = np.array([[3.4, 1.3], [3.2, 0.8]])
y_outliers = np.array([0, 0])
Xo1 = np.concatenate([X, X_outliers[:1]], axis=0)
yo1 = np.concatenate([y, y_outliers[:1]], axis=0)
Xo2 = np.concatenate([X, X_outliers[1:]], axis=0)
yo2 = np.concatenate([y, y_outliers[1:]], axis=0)

svm_clf2 = SVC(kernel="linear", C=10**9)
svm_clf2.fit(Xo2, yo2)

plt.figure(figsize=(12,2.7))

plt.subplot(121)
plt.plot(Xo1[:, 0][yo1==1], Xo1[:, 1][yo1==1], "bs")
plt.plot(Xo1[:, 0][yo1==0], Xo1[:, 1][yo1==0], "yo")
plt.text(0.3, 1.0, "impossible!", fontsize=24, color="red")
plt.xlabel("legnth", fontsize=14)
plt.ylabel("width", fontsize=14)
plt.annotate("outlier",
             xy=(X_outliers[0][0], X_outliers[0][1]),
             xytext=(2.5, 1.7),
             ha="center",
             arrowprops=dict(facecolor='black', shrink=0.1),
             fontsize=16,
            )
plt.axis([0, 5.5, 0, 2])

plt.subplot(122)
plt.plot(Xo2[:, 0][yo2==1], Xo2[:, 1][yo2==1], "bs")
plt.plot(Xo2[:, 0][yo2==0], Xo2[:, 1][yo2==0], "yo")
plot_svc_decision_boundary(svm_clf2, 0, 5.5)
plt.xlabel("length", fontsize=14)
plt.annotate("outlier",
             xy=(X_outliers[1][0], X_outliers[1][1]),
             xytext=(3.2, 0.08),
             ha="center",
             arrowprops=dict(facecolor='black', shrink=0.1),
             fontsize=16,
            )
plt.axis([0, 5.5, 0, 2])

plt.show()

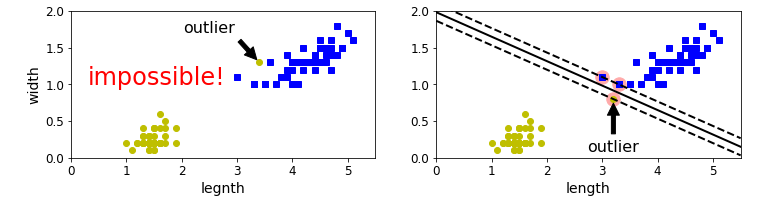
image

앞에서 언급했던 대로 결정 경계를 정하면, 필연적으로 이상치에 민감하게 됩니다. 왼쪽의 경우처럼 다른 클래스 군집사이에 이상치가 섞여 들어가는 경우 아예 결정 경계를 정할 수가 없고, 클래스 군집에서 멀리 떨어진 이상치가 있다면 그 떨어진 만큼 도로의 폭이 좁아지게 됩니다. 따라서, 다음의 소프트 마진 분류 모델이 필요합니다.

4. 소프트 마진 분류

이 모델에는 하이퍼파라미터 C가 있습니다. 하이퍼파라미터 C를 키우면 더 강한 규제를 하고, 줄이면 더 약한 규제를 합니다. 이 말의 의미는 그림을 통해 이해하면 쉽습니다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

plt.figure(figsize=(12,3.2))
plt.subplot(121)
plt.plot(X[:, 0][y==1], X[:, 1][y==1], "g^", label="Iris-Virginica")
plt.plot(X[:, 0][y==0], X[:, 1][y==0], "bs", label="Iris-Versicolor")
plot_svc_decision_boundary(svm_clf1, 4, 6)
plt.xlabel("length", fontsize=14)
plt.ylabel("width", fontsize=14)
plt.legend(loc="upper left", fontsize=14)
plt.title("$C = {}$".format(svm_clf1.C), fontsize=16)
plt.axis([4, 6, 0.8, 2.8])

plt.subplot(122)
plt.plot(X[:, 0][y==1], X[:, 1][y==1], "g^")
plt.plot(X[:, 0][y==0], X[:, 1][y==0], "bs")
plot_svc_decision_boundary(svm_clf2, 4, 6)
plt.xlabel("length", fontsize=14)
plt.title("$C = {}$".format(svm_clf2.C), fontsize=16)
plt.axis([4, 6, 0.8, 2.8])

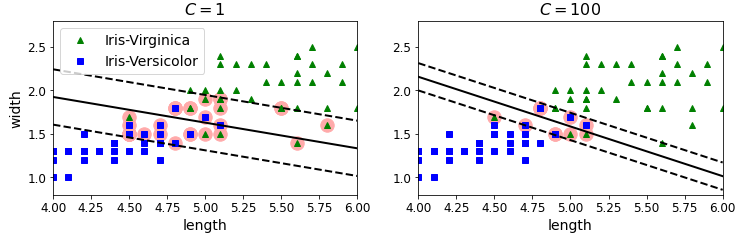
image

왼쪽은 C가 100일 때이고 오른쪽은 C가 1일 때입니다. 왼쪽이 오른쪽에 비해 도로의 폭이 훨씬 좁습니다. C는 도로의 폭과 마진 오류 사이의 균형을 조절합니다. 마진 오류란, 샘플이 결정 경계에 맞지 않는 위치에 있는 경우입니다. 왼쪽의 경우 극단적으로 강한 규제를 가했기 때문에 오른쪽이 더 일반화가 잘 되어 예측 오류가 적다고 합니다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

import numpy as np
from sklearn import datasets
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.svm import LinearSVC

iris = datasets.load_iris()
X = iris["data"][:, (2, 3)]  # petal length, petal width
y = (iris["target"] == 2).astype(np.float64)  # Iris-Virginica

svm_clf = Pipeline([
        ("scaler", StandardScaler()),
        ("linear_svc", LinearSVC(C=1, loss="hinge", random_state=42)),
    ])

svm_clf.fit(X, y)
svm_clf.predict([[5.5, 1.7]])
=>array([1.])

이 모델은 붓꽃이 Virginica 품종이면 1, 아니면 0을 할당해 예측하는 모델입니다. 혼공 머신러닝에서는 아직 pipeline을 써보지 않았었는데, StandardScaler를 이런 식으로 연결해 사용할 수 있다는 것을 처음 알게 되었습니다. 앞으로 한 번쯤 pipeline에 관해 공부해볼까 합니다.

마지막으로, SVM과 로지스틱은 같은 분류 작업을 수행하는 모델이지만 SVM에서는 클래스에 대한 확률을 제공하지 않는다고 합니다. 아마 hinge 손실 함수가 확률을 표현하기에는 적합하지 않아서이지 않을까 싶은데, 핸즈온 머신러닝 5장을 끝까지 공부해보고 나서 다시 생각해 보겠습니다.

study
machine learning
This post is licensed under CC BY 4.0 by the author.
Recently Updated
Contents