현재 공부하고 있는 책인 혼공머신러닝에서는 릿지와 라쏘의 이론에 관한 이야기를 가볍게 언급만 하고 넘어갔기에 핸즈온 머신러닝 책을 참고하여 부족한 내용을 보충하며 이해하고자 합니다. 다음 링크는 핸즈온 머신러닝의 구글북스로 연결됩니다.
1. MSE(평균 제곱 오차)
앞서 선형 회귀를 공부하면서 선형 회귀 모델의 모수를 결정하기 위한 방법으로 최소제곱법을 이야기했었습니다. 잔차 제곱의 합을 최소로 만드는 것이죠. 이 잔차 제곱 합에 1/n을 곱하면 MSE(평균 제곱 오차)가 됩니다. 따라서 MSE는 다음과 같이 쓸 수 있습니다.
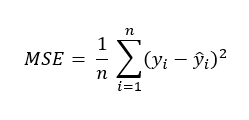
지난 번에는 회귀 모델 평가의 척도로 결정계수만을 언급했지만, MSE 또한 모델 평가에 사용되는 수치입니다. 결정계수는 SSR를 SST로 나누어 전체 변동에 대한 설명변수에 의한 변동의 비율을 알 수 있었다면, MSE는 SSE를 단독으로 평가에 사용하고 있다고 볼 수 있습니다.
MSE와 SSE는 잔차 제곱 합을 전체 데이터 개수 n으로 나누었냐 나누지 않았느냐의 차이인데, SSE는 데이터 개수가 늘어날수록 계속해서 커지게 되기 때문에 이 값만으로는 모델이 어느 정도의 성능을 내고 있는지 절대적으로 알기가 어렵습니다. 따라서 모델을 평가할 때는 SSE가 아닌 MSE나 결정계수를 사용하는 것입니다.
2. 릿지와 라쏘
(1) 릿지
MSE에 관한 설명을 먼저 했던 이유는 릿지와 라쏘의 비용 함수가 MSE에 패널티 항을 더한 형태이기 때문입니다. 먼저 릿지의 비용 함수를 확인해 봅시다.
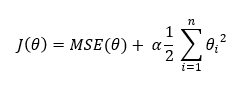
어쨌거나 이 모델의 목표는 비용함수를 최소로 하는 것이기에, 두 개의 식을 더한 형태의 비용함수를 갖게 된 모델은 두 항 중 어느 것을 더 작게 만드는 것에 집중할지를 골라야 합니다. 그것을 정해주는 값이 하이퍼 파라미터 알파입니다.
알파 값이 0에 가깝다면 비용함수는 MSE와 같은 형태가 되어 원래의 선형회귀 식과 동일한 결과가 도출될 것입니다. 반대로 1에 가깝다면 모델은 새로운 규제인 모수 제곱 합을 줄이기 위하여 MSE를 최소로 하는 일에 소홀해질 수밖에 없습니다.
릿지 모델의 모수를 계산하기 위한 방법으로는 정규방정식과 경사 하강법이 있는데, 아직 경사 하강법까지 진도가 나가지 않았기 때문에 정규방정식으로 푸는 방법을 이야기해보려 합니다. 실제로 사이킷런의 릿지 모델은 정규방정식을 사용해 릿지 회귀를 적용합니다. 글에서 정규방정식을 언급하는 것은 처음이지만, 사실 선형회귀 파트에서 이미 정규방정식을 공부하였습니다. 최소제곱법에서 잔차 제곱의 합을 최소로 하기 위해 각 모수로 식을 편미분했던 것이 바로 정규방정식입니다. 특성이 여러 개인 경우, 식을 행렬식으로 바꾸어 행렬미분을 해야 한다는 점이 다를 뿐입니다. 릿지 회귀의 정규방정식은 다음과 같습니다.
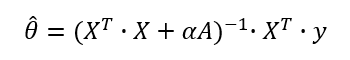
실제 모델은 오른쪽 역행렬을 왼쪽 변과 오른쪽 변에 곱한 후 왼 변을 숄레스키 분해하여 해를 구합니다. 이 역행렬은 X 행렬의 제곱과 특성의 크기 p를 갖는 단위행렬의 합이므로 숄레스키 분해를 위한 전제조건을 만족합니다.
(2) 라쏘
라쏘 회귀의 원리는 릿지와 상당히 유사합니다. 비용함수에 더해지는 값이 제곱이 아니라 절댓값이라는 점이 유일한 차이점입니다.
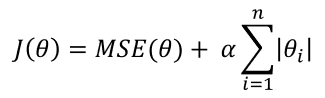
다만, 이 패널티 항의 차이가 가져오는 릿지와 라쏘의 몇 가지 차이점이 있습니다. 우선, 라쏘는 정규방정식으로 해를 찾을 수가 없습니다. 절댓값 항을 처리할 수가 없기 때문입니다. 이 때문에 다른 방법을 사용해서 해를 찾는다고 하는데, 그 방법까지는 공부하지 않았습니다. 다음으로, 라쏘는 모수를 0으로 만들 수 있고, 릿지는 그럴 수 없습니다. 이 차이점의 원인은 패널티 항을 그려보면 알 수가 있는데, 간단히 말하자면 절댓값들의 합을 일정 범위 내로 규제할 때는 그래프가 다이아몬드 모양이 되고, 제곱 항들의 합을 일정 범위 내로 규제할 때는 원 모양이 되는 데서 오는 차이입니다. 라쏘의 경우 패널티 항의 범위와 MSE 타원의 범위가 교차하는 부분이 다이아몬드의 꼭짓점이 되는데, 이 점은 모수 축 위에 있으므로 모수를 0으로 만드는 것입니다. 따라서 라쏘를 사용할 경우 규제를 강하게 할수록 중요하지 않은 특성 순으로 0이 되면서 일부 특성만 사용을 하게 됩니다.
이 라쏘와 릿지에 관한 이야기들은 책만으로는 설명이 부족하여 아래 영상을 나름대로 이해하여 적어 본 것인데, 영상에 자세하고 명료하게 설명되어 있으니 설명이 부족하다고 느끼셨다면 꼭 한 번쯤 시청하시기를 권합니다.
[핵심 머신러닝] 정규화 모델 1
[핵심 머신러닝] 정규화 모델 2
3. 엘라스틱넷
혼공 머신러닝 책에서는 엘라스틱넷을 소개하지 않지만, 핸즈온 머신러닝에서는 이 모델을 다루었기에 마지막으로 엘라스틱넷에 관해 설명드리고 글을 마치고자 합니다. 엘라스틱넷은 릿지와 라쏘를 혼용한 모델로, 비용 함수에 릿지와 라쏘의 패널티 항을 모두 가지고 있습니다.
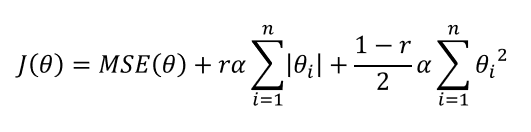
알라스틱넷은 릿지와 라쏘에서 사용하는 하이퍼 파라미터 알파 외에도 하이퍼 파라미터를 한 개 더 가지는데, 이 하이퍼 파라미터로 릿지와 라쏘 간의 비율을 조정합니다. r=0일 때 릿지 회귀와 같은 비용 함수를 가지며, r-1일 때 라쏘 회귀와 같은 비용 함수를 가집니다. 이 모델은 특성 수가 훈련 샘플 수보다 많거나 특성 사이의 상관계수가 높을 때 문제를 일으키는 라쏘를 보완할 수 있어 이런 경우에 용이하게 사용할 수 있습니다.