이번 챕터에서도 조금 더 구체적이고 수학적인 이해를 위해 핸즈온 머신러닝 책과 지난 번에 명료한 설명이 좋았던 강의를 듣고 다시 정리를 해두려 합니다. 영상 출처를 첨부합니다.
[핵심 머신러닝] 로지스틱회귀모델 1
https://www.youtube.com/watch?v=l_8XEj2_9rk&t=2s
[핵심 머신러닝] 로지스틱회귀모델 2
https://www.youtube.com/watch?v=Vh_7QttroGM
로지스틱 회귀는 회귀라는 이름을 가지고 있지만, 실은 분류 문제에서 사용하는 모델입니다. 다만, 그 결과는 시그모이드 또는 소프트맥스 함수에 들어간 상태로 도출되어 확률을 알 수 있다는 점이 지금껏 배웠던 모델들과의 차이점입니다.
1. 시그모이드 함수
시그모이드 함수의 수식과 그래프는 다음과 같습니다.
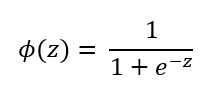

이 함수의 특별한 점은 이전 포스팅에서 언급했지만, 정의역은 모든 실수이고, 치역은 0에서 1까지로 값을 압축하는 역할을 수행할 수 있다는 점입니다. 0보다 작은 수는 0보다 크고 0.5보다 작은 수로, 0일 때는 0.5, 0보다 큰 수는 0.5 보다 크고 1보다 작은 수로 압축됩니다.
시그모이드 함수에 선형 식을 넣으면 다음과 같이 표현됩니다.
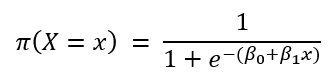
2. 로지스틱 회귀에서 모수의 의미
파이함수는 시그모이드와 선형 식의 합성 함수입니다. 이것이 로지스틱 회귀의 이진 분류에 사용되는 함수입니다. 이 값은 각 데이터 별로 1의 타겟값을 가질 확률이기도 합니다. 척 봐도 선형적이지 않은 이 함수에서 모수를 추정하기는 어려워 보입니다. 또한, 모수의 변화가 이 함수에서 어떤 의미를 가지는지도 알기 어렵습니다. 따라서, 무언가 작업이 필요합니다.
영상에서는 로지스틱 회귀를 설명하기 위해 승산을 먼저 정의하였습니다. 성공 확률을 p라 할 때 승산은 다음과 같이 표현할 수 있습니다.
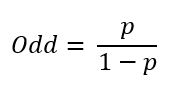
즉, 말로 표현하자면 사건의 실패 확률 대비 성공 확률이라 부르면 됩니다. 갑작스럽게 승산을 이야기하는 이유는 확률 p에 파이함수를 대입하여 로그를 씌우면 선형식이 도출되기 때문입니다.
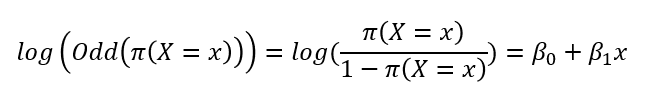
이것을 이용하면 모수의 의미를 정의할 수 있습니다. log함수 안의 값을 odds라 하면, 기울기의 정의를 그대로 사용해 x가 한 단위 증가했을 때 log(odds)의 증가량이 되는 것입니다.
3. 로지스틱 회귀에서 모수 추정하기
로지스틱 회귀에서 모수를 구하기 위한 방법으로 최대 우도 추정법 또는 Cross entropy를 최소화하는 방법을 사용합니다. 사실 둘은 같은 의미입니다.
먼저 최대 우도 추정법을 살펴봅시다. 최대 우도 추정법을 적용하기 위해서는 우도를 먼저 구해야합니다. 우도는 일반적으로 다음과 같이 구합니다.

여기에 쓰인 f는 확률질량함수로, 로지스틱 회귀의 확률질량함수는 이진 분류의 경우 1과 0의 경우의 수만이 존재하기 때문에 베르누이 시행에 따라 다음과 같이 쓸 수 있습니다.
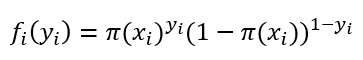
타겟이 1일 때에는 파이함수의 값에 따르고, 0일 때는 1-파이함수의 값에 따르니 확률질량함수의 정의에는 문제가 없습니다. 이제 이 함수를 이용해 우도를 구해봅시다.
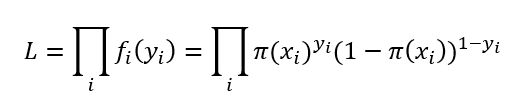
문처럼 생긴 기호는 i를 1부터 n까지 모두 곱한다는 것으로 시그마의 곱하기 버전으로 생각하시면 됩니다. 이때 알아둬야 할 것은 위의 결합확률질량함수를 확률질량함수끼리의 곱으로 표현한 것에는 설명변수끼리의 독립성이 가정되어 있어야 한다는 것입니다. 이렇게 구한 우도에 ln을 씌우면 곱이 합으로 바뀌어 계산이 훨씬 수월해집니다.

그러나, 계산을 편리하게 바꾸었음에도 불구하고 이 경우에는 비선형 모델이기 때문에 이전에 배웠던 정규방정식을 사용해 문제를 풀 수는 없고 다른 방법을 사용한다고 합니다. 다음 기회에 이런 방법들에 관해 공부해 보고 싶습니다.
이제 Cross entropy에 관해 알아봅시다. 사실, 혼공머신러닝 책에서 비용 함수로 Cross entropy를 이미 소개하였습니다. 책에서 설명한 방법으로 Cross entropy를 유도해도 문제가 없지만, 로그를 씌운 우도함수에 -1/n을 곱한 것으로 생각해도 됩니다. -가 붙었기 때문에 반대로 최대가 아닌 최소를 찾아야 하는데, 값이 작을수록 더 뛰어난 성능의 증명이 되어야 하는 비용함수의 특성 때문에 곱한 것 같습니다.